1. 부울 스위칭 대수
- 부울 대수 : 논리 연산자 and, or, not을 사용하여 논리적 기능을 처리하는 논리 수학
- 부울식 : 논리적 기능을 기호로 나타낸 식
- 논리변수 : 시간에 따라 변하는 논리치를 갖는 양
- 논리연산자 : 논리 시스템을 해석하고 설계하는데 사용되는 기본적인 기능
- 논리함수 : 임의의 시스템이 갖고있는 논리적인 기능
- 진리표 : 모든 가능한 경우의 논리적인 입력과 출력과의 관계를 나타낸 표
2. 부울 함수
- Closure : + /· (and / or)
- 단위원 (identity element) : 원래 꼴이 나오게 만드는 값 (or일 때는 0, and 일 때는 1)
ex) x+0 = 0+x = x
x · 1 = 1 · x = x
- 교환법칙, 분배법칙
- 보수
ex) x + x' = 1
x · x' = 0

ex) F1 = x + y'z ,
F2 = x'y'z + x'yz + xy' = x'z(y'+y) + xy' = x'z + xy'



* 부울 함수를 리터럴의 개수가 최소가 되도록 간략화하기!
* 쌍대의 법칙 : and를 or로, or을 and로 싹 다 바꾸면 값이 같다.
* 함수의 보수 : 드모르간 법칙과 굉장히 유사... (A+B+C)' = A'B'C' -> 쌍대 구해서 각 리터럴을 보수화하면 됨
3. Canonical and Standard Forms
1) Canonical Forms
- Minterm : 이진 변수에 대한 AND의 항(표준 곱) -> n개의 변수에 대해서 2^n개 있음
- Maxterm : 이진 변수에 대한 OR의 항(표준 합) -> 얘도 2^n개 있음

Minterms에서는 and 연산한 결과가 무조건 1이 나오도록 변수를 지정해주고, Maxterms에서는 or 연산한 결과가 무조건 0이 되도록 지정해준다고 생각하면 됨.

minterm은 함숫값이 1이 되는 걸 기준으로, maxterm은 0이 되는 것을 기준으로 함.
- Sum of Minterm
ex) 부울함수 F=A+B'C를 minterm의 합으로 표시
A = A(B+B') = AB+ AB' = AB(C+C') + AB'(C+C') = ABC+ABC'+AB'C+AB'C'
B'C = (A+A')(B'C) = AB'C+A'B'C
따라서 ABC+ABC'+AB'C+AB'C'+AB'C+A'B'C = A'B'C+AB'C'+AB'C+ABC'+ABC = m1 + m4+ m5 + m6 + m7 = ∑(1,4,5,6,7)
- Product of Maxterm
ex) 부울함수 F= xy+x'z를 maxterm의 곱으로 표시
F = xy+x'z = (xy+x')(xy+z) = (x+x')(y+x')(x+z)(y+z) = (x'+y)(x+z)(y+z)
x'+y=x'+y+zz' = (x'+y+z)(x'+y+z')
x+z=x+yy'+z=(x+y+z)(x+y'+z)
y+z=xx'+y+z=(x+y+z)(x'+y+z)
이하 생략
- Conversion between Canonical Forms
F(A,B,C) = ∑(1,4,5,6,7)
F'(A,B,C) = ∑(0,2,3)
F = (m0 + m2 + m3)' = m0'm2'm3' = M0M2M3
즉, mj ' = Mj
2) Standard Forms ; 리터럴을 최소화하자!
- Sum of product (SOP) : F1 = y' + xy + x'yz'
- Product of sum (POS) : F2 = x(y'+z)(x'+y+z'+w)

4. 2진 논리함수
-AND 게이트

-OR 게이트

-NOT 게이트

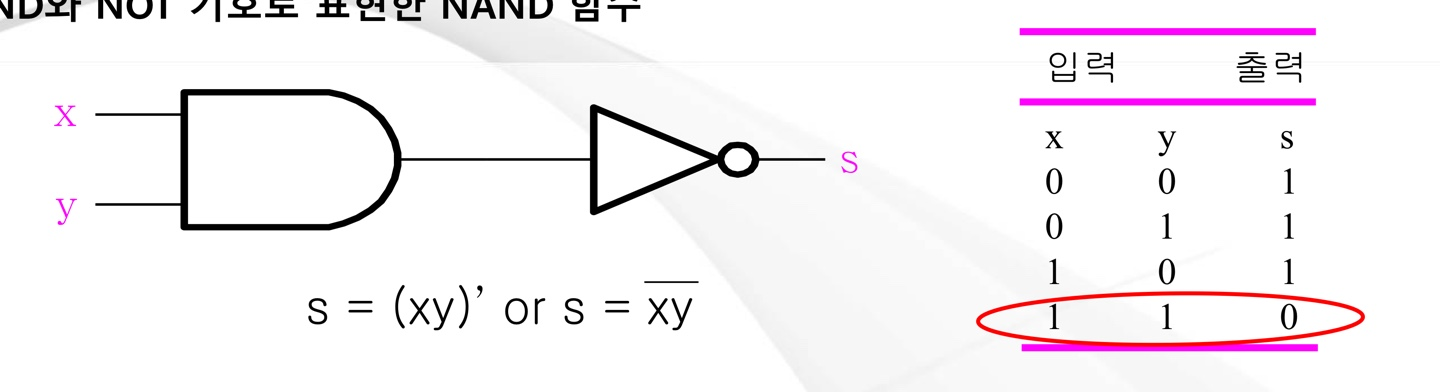
- NAND 함수 : s = (xy)' = x' + y'

- NOR 함수 : s = (x+y)' = x'y'


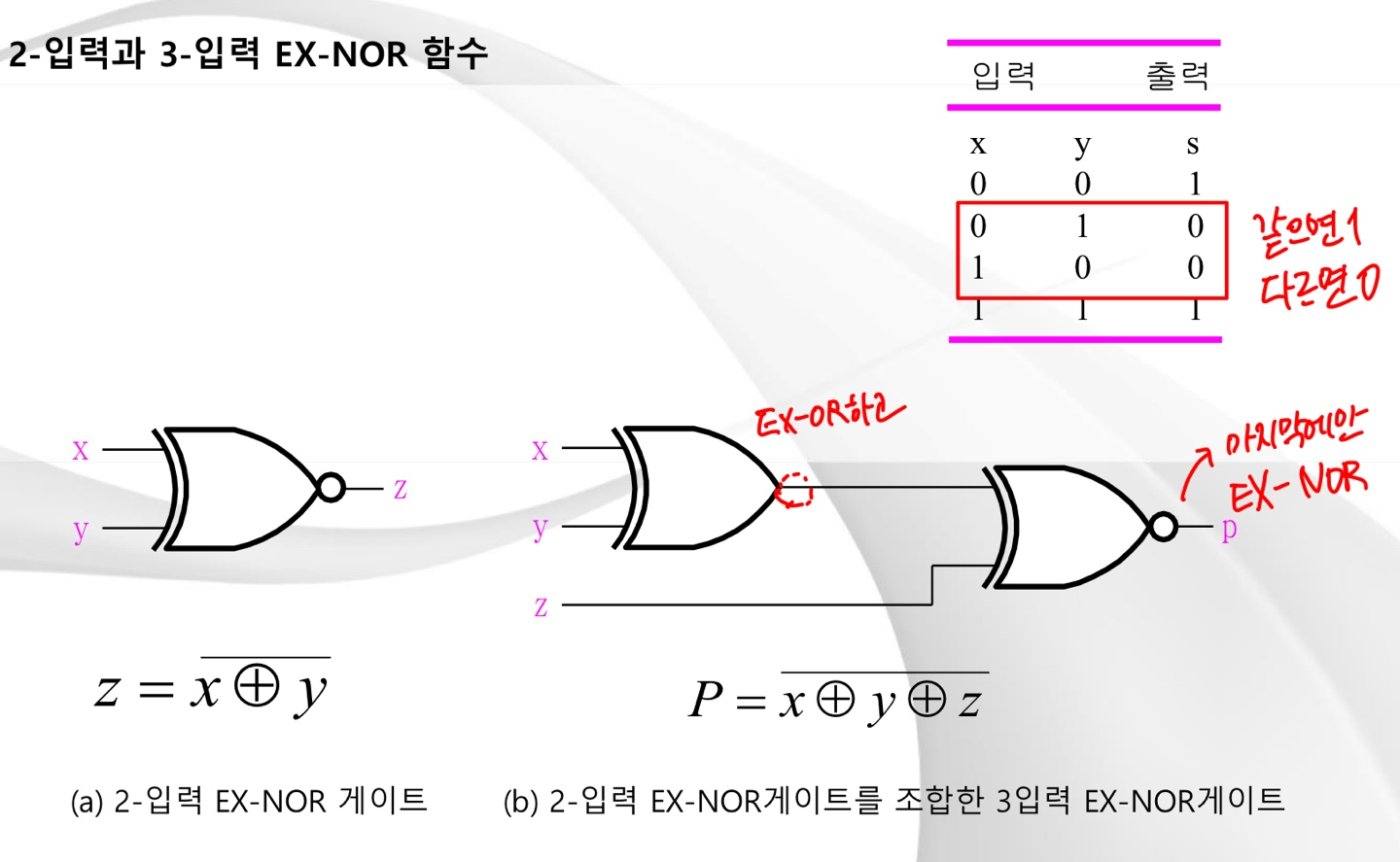
- EX-OR 함수 (XOR) : 같으면 0 다르면 1!

- EX-NOR : 같으면 1, 다르면 0
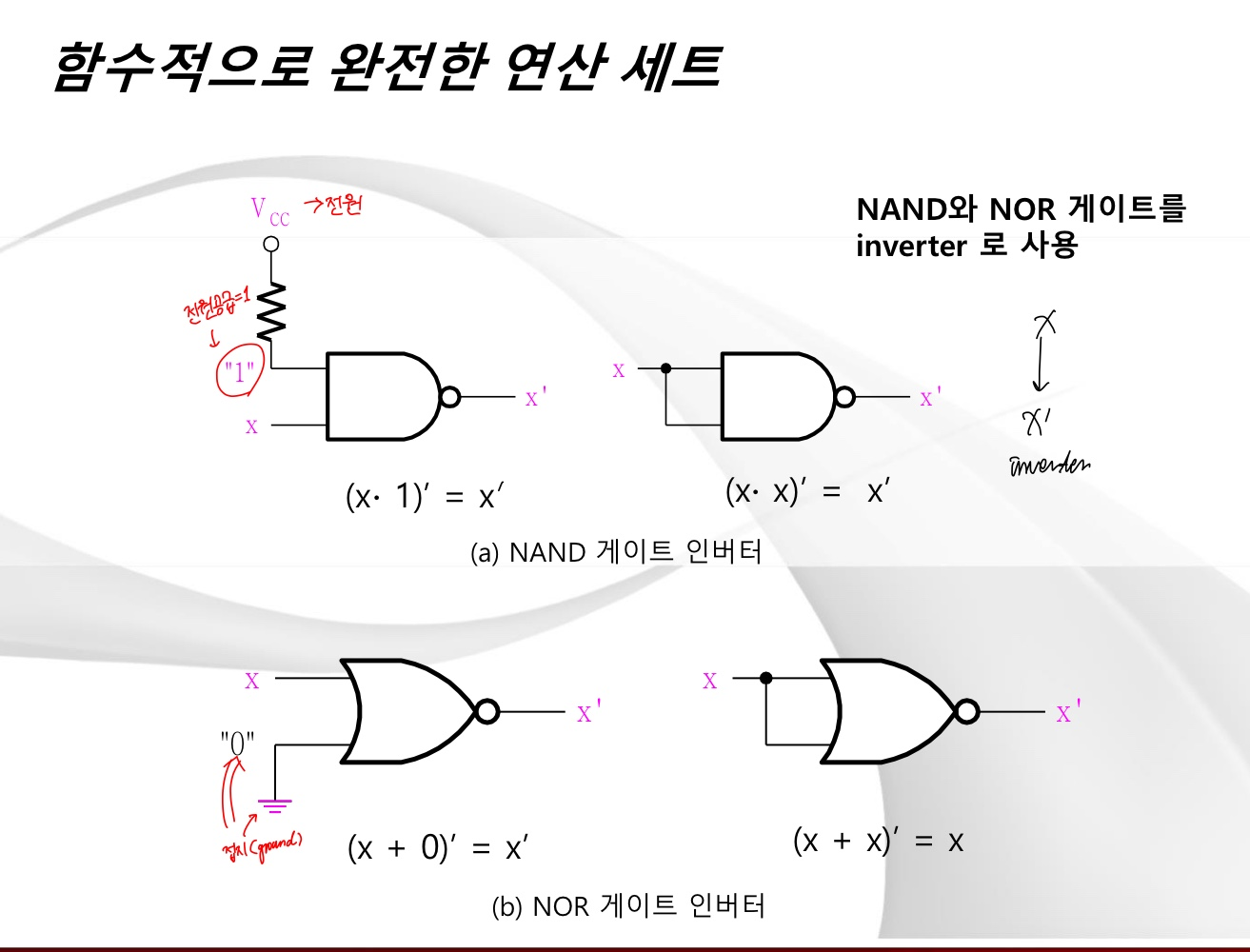

(1) ((xy)')' + ((xy)')' = x'+y')' + (x'+y')' = xy + xy = xy
(2) (x')' + (y')' = x + y
'𝓡𝓸𝓸𝓶5: 𝒦𝑜𝓇𝑒𝒶 𝒰𝓃𝒾𝓋 > 논리설계 Digital Design(COSE221)' 카테고리의 다른 글
| [논리설계] Verilog-HDL 설계 (0) | 2021.04.29 |
|---|---|
| [논리설계] 1. 디지털 시스템과 2진수체계 (0) | 2021.04.29 |
