1. Relations
- 주어진 집합 X, Y에서 Cartesian product X x Y 를 하면 그 결과는 x∈X, y∈Y인 (x, y)의 모든 ordered paris 이다.
X x Y = {(x,y) | x∈X and y∈Y}
-Binary relation (이진 관계) : 두 집합의 원소 사이의 관계
집합 X 에서 집합 Y 로의 binary relation R은, Cartesian product X x Y 의 subset(부분집합)이다.
Ex) X = { 1, 2, 3 } and Y = { a, b }
R = {(1, a), (1, b), (2, b), (3, a)} 는 X와 Y 사이의 relation이다.
- Domain : y∈Y인 y에 대하여 (x, y)가 relation R에 속할 때, x∈X인 x를 Dom(R)이라고 한다.
Dom(R) = { x∈X | (x, y) ∈ R for some y∈Y }
Range : x∈X인 x에 대하여 (x, y)가 relation R에 속할 때, y∈Y인 y를 Rng(R)이라고 한다.
Rng(R) = { y∈Y | (x, y) ∈ R for some x∈X }
쉽게 생각해 함수에서 정의역과 치역이라고 생각하면 된다.
f(x)에서 x의 범위가 정의역, 그에 따른 y의 값의 범위가 치역이었던 것처럼 relation도 마찬가지!
Ex) X={ 1, 2, 3 } , Y={ a, b }, R = { (1, a), (1, b), (2, b) }
일 때 Dom(R) = { 1, 2 }, Rng(R) = { a, b }
- digraph of a relation : relation의 유향 그래프 (방향이 있는 그래프)

- Properties of relations
1) Reflexive : 모든 x∈X에 대해서 (x,x)∈R인 relation, 즉 자기 자신을 항상 가리키는 relation
2) Symmetric(대칭) : 모든 x, y가 (x, y)∈R 이면 (y, x)∈R인 relation
3) transitive (전이(추이)관계) : (x, y)∈R이고 (y, z)∈R이면 (x, z)∈R이 되는 relation
4) antisymmetric (반대칭적) : x ≠ y일 때, (x, y)∈R이면 (y, x)는 relation에 속하지 않는 것.
즉, (a, a)를 제외하고 (a, b)가 R에 속했으면 (b, a)는 속해있으면 안됨
- Order relations
1) Partial order : R이 reflexive, antisymmetric, transitive하면 이 R은 partial order이다.
ex) (x, y) in R (y는 x로 나누어 떨어지고, x와 y는 양의 정수)
--> (5, 10), (5, 15), (5, 20), (10, 20)
- 모든 양의 정수는 자기 자신으로 나누어 떨어지므로 reflexive
- (a, n*a)가 성립할 경우 (n*a, a)는 성립할 수 없으므로 antisymmetric
- (a, n*a)이고 (n*a, m*na)일 경우 (a, mna) 이므로 transitive
2) Comparable : (x, y) or (y, x)가 R에 존재하면 x와 y는 comparable하다.
Incomparable : (x, y)와 (y, x)가 둘 다 R에 있지 않으면 incomparable하다.
3) Total order : X에 있는 elements의 모든 쌍이 comparable하면 R은 total order on X이다.
즉, X에 있는 모든 원소가 R에 존재할 경우 R은 X의 total order 이다. (모든 (x, y)가 포함되어 있되, 순서 바꿔서 겹치면 안된다(antisymmetric 해야하기 때문))
ex) (x, y) in R ( x ≤ y, x와 y는 양의 정수 )
- Inverse of a relation
: 주어진 relation R이 X->Y 였다면, 그것의 inverse인 R^(-1)은 Y-X인 relation이다.
R^(-1) = { (y, x) | (x, y)∈R }
(그냥 역함수 생각하면 편하다)
- Composition of relation
: R1 : relation from X to Y
R2 : relation from Y to Z
R2ºR1 (composition of R1 and R2) : relation from X to Z
-> R2ºR1 = { (x, z) | (x, y)∈R1 and (y,z)∈R2 for some y∈Y}
2. Equivalence Relations
- Equivalence relation on X = R은 reflexive하고 symmetric 하고 transitive하다
ex) X를 정수라고 하고, R을 X에 대한 relation이라고 하자. xRy <=> x-y = 5k (k는 정수)
==> R is and equivalence relation
{ ..., (10, 5), (11, 6), (5, 5), (6, 11), (5, 10) ,... }
x - y = 5k 면 y - x = -5k
x = y 면 x - y = 0
x3 - x2 = 5k1, x2 - x1 = 5k2 면 x3-x1 = 5(k1-k2)
- Partition S : X를 이루는 부분집합들의 모임 {A1, A2 ,..., An}
A1∪A2∪A3∪A4∪...∪An=X
단, 1<=j, k<=n이고 서로 다른 모든 j, k에 대해 Aj ∩ Ak = ø
ex) X= {정수} , E = {짝수), O = {홀수} 이면 S = { E, O } 는 X의 partition
- Equivalence relation : S를 집합 X의 partition이라고 할 때, R을 xRy라는 relation으로 정의하자. R에서 x, y가 T∈S인 T 집합에 속할 때, R은 X에 대해 equivalence relation이다.
이게 대체 무슨 소린지 한참을 들여다 봤는데, 예를 들어보자.
X의 partial S가 있다. 이 S는 A1, A2, A3의 부분집합들을 갖는다. 만약 어떤 relation xRy가 A1이라는 T 집합에만 속한 x, y를 전부 포함한 relation이라면 이 relation은 X의 equivalence relation인 것이다.
왜냐?
예를 들어 "x-y = 2k"라는 relation R이 있다.
xRy는 만약 x와 y가 같은 partition(T= even or odd) 에 있을 때 true가 된다. (X의 partition S = Integer, S = E + O)
이 때 이 R은 X의 equivalence relations 이 된다. 정리하면, 같은 partition 안의 요소끼리 relation을 만드는, 그래서 relation 안에 partition의 element가 전부 포함된 relation은 equivalence relation인 것. (사실 이해 안하고 위에 reflexive, symmetric, transitive 특징 쓰는게 더 나을 듯 싶다..)
- Equivalence classes : 집합 𝑨 에 대한 관계 𝑹 이 동치관계(Equivalence Relation) 일 때, 집합 𝑨 의 각 원소 𝒂 와 순서쌍을 이루는 원소들의 집합 [a]
a, b ∈ X 이면 [a] = [b] 이거나 [a] ∩ [b] = ø 이다.
ex) Even Integer : [2] = [4] = [10002]
이것도 뭔소린가 했더니, 그냥 [a]라는 것이 있으면, [a]는 a라는 element가 속한 partition의 원소들의 집합, 즉 그 partition을 말하는 것이다. 그래서 [2]=[4]=[10002]는 전부 even integer라는 integer의 partition이라는 말씀.
만약 a와 b가 둘 다 X에 속하게 되면 둘 다 같은 partition에 속해 [a]=[b]가 되거나, 서로 다른 partition에 속해 [a]와 [b]의 교집합이 존재하지 않게 된다.
3. Matrices of Relations
: Relation을 Matrices로 표현해보자!
- 행은 X의 elements로, 열은 Y의 elements로, Aij = 0 이면 not related, 1이면 related!

- The Product of matrices ( 행렬의 곱 )
: R1의 Matrix A(l x m)과 R2의 Matrix B(mxn)을 곱하면 ?
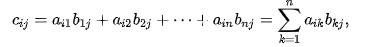
이 때, 곱한 값이 0이 아니면 1, 0이면 0이다. 이걸 언제 쓰냐?
-> R2ºR1 (composed relation)을 계산할 때 쓴다.
- Matrix로 알아보는 relation의 특징들
1) Reflexive : 모든 Aii의 값이 1이다
2) Symmetric : 모든 i, j에 대해 Aij = Aji 이다.
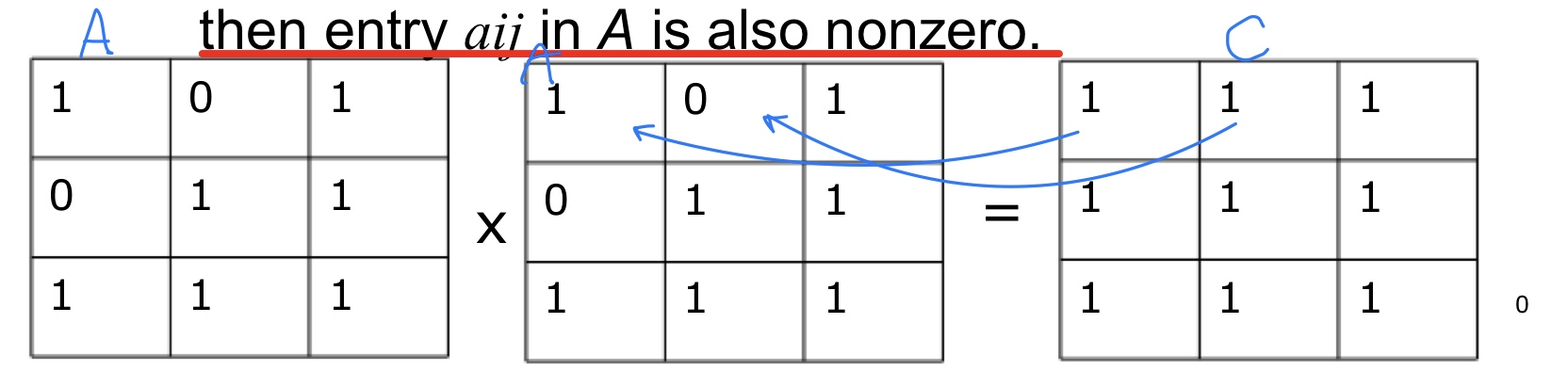
3) Transitive : C = A^2(=AxA)의 Cij가 0이 아니면, A의 aij도 0이 아니다.
4. Relational Database
'𝓡𝓸𝓸𝓶5: 𝒦𝑜𝓇𝑒𝒶 𝒰𝓃𝒾𝓋 > Discrete mathematics' 카테고리의 다른 글
| [이산수학] Chapter 1. Logic and proofs (0) | 2021.05.03 |
|---|---|
| [이산수학] Chapter 6. Counting methods and the pigeonhole principle (0) | 2021.05.02 |
| [이산수학] Chapter 5. Introduction to Number Theory (0) | 2021.05.02 |
| [이산수학] Chapter 4. Algorithms (0) | 2021.04.07 |


