3. Theorem Proving
: Theorem Proving이란 우리가 이미 알고있는 사실(Knowledge base)의 sentence들에 추론 규칙(Inference rule)을 적용해서 새로운 사실을 알아내는 것/ 새로운 문장을 만들어내는 것을 말한다.
만약 model의 개수가 많고, proof의 길이가 짧다면, theorem proving이 model checking보다 더 효율적이다.
1) Inference Rules
- Modus Ponens : α⇒β이고 α가 true면 β도 true다.

- And-Elimination : α and β가 true이면 α는 항상 true이다

- Logical equivalences : α and β가 true이면 β and α도 true이다.


- α 와 β가 같은 model의 집합에서 true일 때 logically equivalent하다고 말하고 α ≡ β라고 쓴다.

자 그럼 이걸 이용해서 Wumpus world 문제를 풀어내보자.

먼저 기본적으로 알고 있는 것들 (R1~R5)을 적어준다. 그런 다음 이 아이들끼리 붙이고 합치고 전개하고 나누고 난리를 치다보면 R6~R10의 새로운 논리식들이 등장하게 된다. 이것들은 모두 inference rule 을 써서 도출해낸 것이므로 전부 참이다. 우리가 구하고자 하는 (1,2) 와 (2,1)은 함정이 없다는 결론이 나왔다.
그렇다면 어떤 sentence에 어떤 inference를 적용할지는 어떻게 정할 것인가?
그 방법 중 하나가 바로 State Space Search이다.
* State Space Search
: KB를 초기 상태로 두고 각각의 sentence에게 가능한 모든 inference rule을 적용시켜 result를 추가해나가며 goal이 나올 때까지 반복해서 찾는 것
- initial state : the initial Knowledge Base
- Actions: 모든 sentence에 inference rule을 적용
- Results : inference rule로 나온 새로운 문장으로, 이 새로운 문장은 KB에 추가한다.
- Goal : 우리가 증명할 sentence를 포함한 state
되게 비효율적인 것처럼 보이고 그냥 이럴거면 model을 다 나열해서 model checking하는거랑 별반 다를게 없지 않나 싶지만, 사실 이 proof는 goal과 관련이 없는 명제들은 무시하고 시작하기 때문에 굉장히 efficient하다.
- Modus Ponens 와 And-Elimination은 sound하다. 이 밖에도 다른 추론 규칙들 모두 당연히 sound하다. 따라서 굳이 모든 model을 나열해보지 않아도 sound하다는 것을 알 수 있다.
- search 알고리즘도 iterative deepening search처럼, goal이 도달 가능하다면 complete하다. 그러나 만약 사용 가능한 inference rule이 적절하지 않으면, 즉 내가 쓸 수 있는 inference rule 이 아닌 다른 rule이 증명에 필요하다면 goal에 도달할 수 없다. 때문에 무조건 complete한 것은 아니다.
- Monotonicity (단조성)
: 이 logical system의 가장 큰 특징 중 하나가 바로 monotonicity이다. KB에 정보들이 추가되면 될 수록, entail 될 수 있는 문장들도 따라서 증가한다. 아무 문장 α 와 β에 대해 다음과 같은 식이 만족한다.

KB가 α 를 entail 한다면, KB ∧ β 역시 α를 Entail한다. 즉 KB에 문장이 추가된다고 하더라도 entail 될 문장들이 갑자기 안되고 뭐 그럴 일은 없다는 얘기다. 즉 β는 α의 entail 여부와 관계가 없다.
2) Resolution Rules :
inference rule 여러개 필요 없어! 규칙 하나면 충분해! Complete하게 만들어줄게!
① Unit resolution rule
- literal들이 disjunction으로 연결되어있는 Clause와, 그것의 complementary literal이 있다고 생각해보자.
complementary literal이란, clause 안에 들어있는 아무 literal 중 하나에 not이 붙은 literal을 말한다.
Clause와 complementary literal이 둘 다 참이라면, complementary literal과 짝이 되는 literal이 clause에서 빠져도 여전히 true라는 이야기이다.
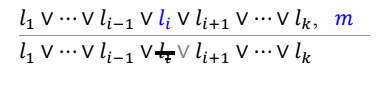
여기서 Li와 m이 complementary 한 관계다. 즉 clause에서 Li이 삭제되어도 여전히 true이다. 왜?
clause는 다 or로 이어진 관계이다. 이미 li가 false임이 드러났기 때문에 li가 아닌 다른 literal에서 true가 나와 clause 전체가 true가 된다는 거다. 그래서 빼도 된다.
② Resolution rule 은 Unit resolution rule의 응용편이다.
두 개의 clause가 있고, 각 clause에는 각각 complementary한 literal이 하나씩 있을 때, 그 두개의 literal을 빼고 두 clause를 합친 clause는 true이다.

-> li와 mj가 complement한 관계이다. li와 mj 둘 중 하나는 false, 하나는 true이므로 나머지 l과 m 중에는 무조건 하나의 true인 값이 존재했을 것이다. 따라서 두 clause를 or로 합치게 되면 여전히 true가 된다.

- resolution rule의 sound함은 뭐 그냥 당연하다. 진리표를 그려봐도 그렇고 논리적으로도 그렇고 그냥 resolution은 sound하다.

아까 위에서 R10까지 했었다. 구냥 눈으로 쭉 읽으면서 따라가자.
R15에서 R13과 Resolution을 하면 해당 literal이 사라지고 R16이 되었다. 여기서 또 R1이랑 resolution을 하면 R17까지 구할 수 있다.
자 지금까지 dclause 끼리의 KB에서 적용되는 resolution에 대해 배웠다. 근데 만약 명제가 clause의 형태가 아니라면?? 만들어주면 된다!
3) Conjunctive Normal Form
: 어떤 sentence를 conjunction of clause(clause들의 곱)로 나타내는 것을 Conjunctive Normal Form(CNF)라고 한다.
모든 sentence는 conjunction of clause와 논리적으로 동치이기 때문에 잘 변형하면 CNF로 만들 수 있다.
① Biconditional elimination을 이용해 ⇔ 기호를 다 없앤다 (α ⇔ β) ≡ (α ⇒ β)∧(α ⇒ β)
② Implication elimination을 이용해 ⇒ 기호를 다 없앤다 (α ⇒ β) ≡¬α ∨ β
③ double-negation elimination과 de morgan 법칙을 써서 ¬ 기호를 모두 괄호안으로 넣어준다.
④ distributivity law를 사용해서 ∧를 괄호 밖으로, ∨을 괄호 안으로 넣어준다.

그러면 위의 사진처럼 Or 로 엮인 Clause들이 and로 이어지는 모양을 하게 된다.

4) Resolution Algorithm
- Satisfiability and Validity
한 문장이 어떤 model에 의해서 satisfied되거나 true일 경우, 이 문장은 satisfiable하다. 즉, "어떤" model에 대해서 sentence가 true이면 satisfied한 것이다.
satisfiability를 확인하기 위해서는 하나라도 문장을 만족시키는 model이 있는지 찾아보면 된다. 그리고 명제 추론을 통해 이 setence의 satisfiability를 결정하는 문제를 SAT problem이라고 한다.
또한 어떤 문장이 모~든 Model에 대해 true 일 때 이 문장은 valid하다고 한다.

따라서 α가 satisfiable 하다는 얘기는 ¬α가 valid하지 않다는 것을 의미한다.
¬α가 valid하려면 모든 α가 false여야 하는데 α가 satisfiable하다는 것은 최소한 하나는 true라는 것을 의미하기 때문이다.
반대로 α가 valid하면 ¬α는 unsatisfiable하다.¬α가 satistiable 하다는 얘기는 α 중 최소한 하나가 false여야 하는 것인데, α가 vaild하다는 얘기는 전부 true라는 얘기이고 따라서 satistiable한 것은 말이 안된다.
- Proof by refutation
갑자기 생뚱맞게 웬 valid 얘기냐 했겠지만,
이걸 한 이유는 α ⊨ β 가 맞는지, α가 β를 entail 하는지 확인하기 위해서 (α ⇒ β)가 모든 model에 대해 true인지를 확인해보면 되기 때문이다. 즉,
α ⊨ β if and only if the sentence (α ⇒ β) is "valid"
이다.
이 증명은 refutation, 즉 귀류법(=proof by contradiction)을 이용해 할 수 있다.
① (α ⇒ β)가 Valid하다 ⇔ ¬(α ⇒ β)가 Unsatifiable하다.
② ¬(α ⇒ β) ≡ (α ∧ ¬β)이므로 α ⊨ β if and only if (α ∧ ¬β) is unsatifiable
따라서 α ⊨ β 가 사실임을 보이기 위해서는 ¬(α ⇒ β), 즉 (α ∧ ¬β) 가 Unsatifiable함을 보이면 된다.
③ 위 식에서 이미 참임을 알고 있는 α에 대해, β가 false라고 가정하면 모순이 발생함을 보이면 된다.
우리가 알고 싶은 것은 KB⊨ α니까, (KB ∧ ¬ α)가 unsatisfiable임을 보이면 된다.
① (KB ∧ ¬ α)를 CNF 로 바꾼다.
② CNF에서 결과로 나온 Clause에 resolution rule을 적용한다. complementary literal을 포함한 pair의 경우 새로운 clause를 생성해낼 것이고, 그 clause가 이미 있는 clause가 아니라면 set에 추가해준다. 그리고 다음 조건을 만족할 때까지 반복한다.
③ 두 clause를 resolve했더니 empty clause가 되었다면 KB는 α를 entail 하는 것이다.
만들대로 만들어서 더이상 추가할 새로운 clause가 없이 끝이 났다면, KB는 α를 entail 하지 않는다.
2번 조건을 보면, CNF로 바꿀 경우 (Clause) ^ (Clause) ^... 의 꼴이 될 것이고, 이 경우 각각의 Clause들이 모두 true여야 한다. 따라서 각 Clause끼리 resolution rule을 적용해 합칠 수가 있다.
3번 조건을 보면, 두 clause를 resolve 했더니 최종적으로 empty clause가 되었다는 얘기는, CNF 안에 complementary한 clause가 있었다는 것이다. P와 ¬P가 동시에 and로 묶여져 있던 것이다. and 연산을 했을 때 절대 그 값이 true가 될 수 없는데, true로 놓고 계산을 하고 있었으니 말이 안된다. 따라서 (KB ∧ ¬ α)가 unsatisfiable 하다.
반면 두 clause를 다 resolve 해서 더이상 더 만들어 낼 clause가 없다는 이야기는 clause끼리 resolve 해서 나올 수 있는 모든 경우를 다 생각해봤다는 이야기이다. 근데 그 모든 경우에 empty clause가 없었으므로 모순되지 않고 true라는 이야기 이다. 그래서 KB는 α를 entail 하지 않는다는 결론을 내릴 수 있다.

clauses에는 (KB ∧ ¬ α)를 cnf 로 나타냈을 때 clause들의 집합이 들어가고
new에는 resolution을 통해 새로 만들어질 clause를 넣어줄 것이기 때문에 공집합으로 초기화를 해준다.
그리고 loop문을 시작한다.
clauses에 포함된 모든 clauses들의 쌍을 대상으로 resolve를 해서 new에 추가해준다. 만약 이 과정에서 중간에 empty clause가 나오면 unsatistiable을 증명한 것이므로 entail하기 때문에 true를 반환해준다.
만약 clauses들에 대해 for문을 마쳤는데, 이 때 새로 나온 new가 이미 존재하는 clauses들에 속한다면 모순이 없으므로 entail 하지 않는다. 따라서 false를 반환한다.
이 모든 if문에 해당사항이 없다면 새로 만든 clauses를 clauses 집합에 추가해주고 또 다시 반복한다.

자 이 예시로 한 번 직접 해보자.
KB는 규칙과, 관측한 값이 들어가 있다.
그리고 내가 궁금한 것은 (1,2)에 함정이 없는가 이다.
따라서 KB가 query를 entail 하는지를 알아보겠다.
일단 저 식을 CNF로 바꾸어 주니 clause가 총 5개가 나왔다.
이 각각의 clause에 모두 resolution을 적용해보면

이러한 결과가 나온다. resolution해서 나올 수 있는 모든 결과를 탐색해보다 보니 중간에 empty clause가 발견되었고, 이 아이는 애초에 말이 안되는, true가 아닌 식이었던 것이므로 entail 한다는 사실을 알 수 있다.
'𝓡𝓸𝓸𝓶5: 𝒦𝑜𝓇𝑒𝒶 𝒰𝓃𝒾𝓋 > Artificial Intelligence(COSE361)' 카테고리의 다른 글
| [인공지능] 8~9. First-Order Logic(FOL) (2) | 2021.04.25 |
|---|---|
| [인공지능] 7. Propositional Logic - 3 (2) | 2021.04.25 |
| [인공지능] 7. Propositional logic - 1 (0) | 2021.04.24 |
| [인공지능] 6. Constraint Satisfaction Problems (0) | 2021.04.24 |
| [인공지능] 5. Adversarial Search(적대적 탐색) (0) | 2021.04.24 |



